序章
統計の目的は、データの裏側にある本質を理解する
一方、統計にだまされないこと、
「世の中には3種類の嘘がある:嘘、大嘘、そして統計だ」
There are three kinds of lies: lies, damned lies, and statistics.
– by Mark Twain
統計には、「記述統計」と「推測統計」がある。
記述統計は、全数調査を前提
記述統計は、データを整理、視覚化することでデータを理解して判断に役立てる
推測統計は、サンプリング調査を前提、部分から全体を知る。
つまり、得た標本から母集団を知る。
仮説が正しいかを判断する。
過去から未来を予測する。

記述統計、推測統計は、確率論と関係が深く、標本集出時のゆらぎを考える必要がある
交絡因子とは、原因と結果の双方に関連して。双方の集団に偏って存在する。
交絡因子の3要件:
(1)結果に影響を与える
(2)原因と関連がある
(3)原因ろ結果の中間因子でない
相関関係(correlation)があるからといって、必ずしも因果関係(causality)があるわけでない。
データ特性、可視化
質的データと量的データ
質的データは、記号を値として取るデータ
-名義尺度 値が単なるラベルとして扱われる。 例:「男」「女」
-順序尺度 順序に意味がある。例 好き>普通>嫌い
量的データは、数値を値として取るデータ
-間隔尺度 数の間隔に意味がある。 例:温度
-比例尺度 数の比にも意味がある。 例:身長
データが取りうる値の範囲をあらかじめ定めた区間(階級:bin)に分け、
集計を行うことを量子化と呼ぶ。
データ、階級、度数(累積度数、相対度数、累積相対度数)など
階級幅の設定
スタージェス (Sturges)の方法: K = log2・N + 1
データが100個: log2・100 + 1 =7.64 ->8階級ぐらい(bin数)
データが 50個: log2・50 + 1 =6.64 ->7階級ぐらい(bin数)
データが 25個: log2・25 + 1 =5.64 ->6階級ぐらい(bin数)
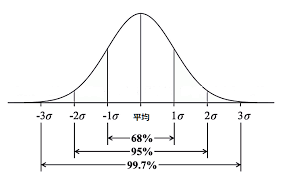
データの特徴を表す数値: 平均値(mean)、最頻値(mode)、中央値(median)
統計ソフトウェア
JMP,SPSS,SAS,STATS
エクセル、Rなど
フリー統計ソフトEZRがおすすめ:
分析の手順:
EZRでデータを読み込む(ファイルー>データインポートー>エクセルインポート)
データの特徴を計算する(統計解析ー>連続変数の解析ー>連続変数の要約ー>数値による要約ー>質的変数)
ヒストグラムを作成する(グラフと表ー>ヒストグラムー>定数の選択)
分割表を作成する(名義変数の解析ー>分割表の作成と* ー>行の選択、列の選択)
EZRのダウンロード:
https://www.jichi.ac.jp/saitama-sct/SaitamaHP.files/statmed.html
2元分割表
集計と解析
調査結果から仮設を検証
集計方法
■カテゴリ|単純集計・クロス集計
■数値|度数・平均・標準偏差
解析方法
■独立性の検定|カイ二乗検定、フィッシャーの直接確率法
一般化マンテル検定、ロジスティックモデルなど
2つの変数が独立ならば、クロス表におけるそれぞれの比率が同じ。
クロス票の差を「カイ二乗値」ではかる。
診断学では、感度・特一・陽性的中率、陰性的中率、偽陽性、偽陰性
事前確率の状況の変化によって、事後の確率は変わってくる。
■平均の差の検定|t検定
■関係性の強さ|オッズ比の推定、相関関係、重回帰分析など
検定・推定
推測統計には、検定と推定がある。
仮説検定とは、標本を元に母集団に関する仮説の真意を調べる。
つまり、標本から分析して、母集団を推測する。
推定は、標本を基に母集団の母数の値を推定する。
点推定|一つの値で推定
区間推定|真の変数の値が入る確率が、一定以上に保証される区間を求める
信頼区間を求める
信頼係数90%の信頼区間は、 Xーα 以上、 X+α以下の範囲
Xーα 以下の5%、 X+α以上 5%の確率で発生する。
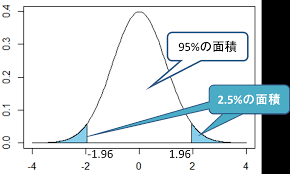
95%信頼区間
比率の差の95%信頼区間 0.06 -0.14が「0をまたいでいない」
差がゼロである可能性は、5%以下
統計学的な有意差がある
統計学的仮説検定
ある仮説が正しいといえるかどうかを統計学的・確率論的に判断するための手法
仮設が正しいと仮定した上で、それに従う母集団からの実際に観察された標本が
抽出される確率を求める
その確率が十分に小さければ(5%以下 OR 1%以下)「仮設はなりたちそうもない」と判断できる
例:
仮設を設けるー>それに反する証拠を挙げる
薬Aと薬Bの有効性にさがあるか?
(1) A とBには差がないと仮定する
(2)Aの有効性 18/20 に対し、Bの有効性 8/25
(3)もし仮定が正しければ、有効性の事象はほとんど起こらない
(4)したがって仮設は誤り ー>AとBの有効性には、差がある。
対立仮説と帰無仮説
対立仮説(alternative Hypothesis) H1:証明したい仮説
帰無仮説 (null hypothesis) H0: 上記を否定する仮設
ー>仮説検定の対象となるのは「帰無仮説」
ー>帰無仮説が棄却される ー>対立仮説が支持される
帰無仮説が棄却されなかったら、必ずしも帰無仮説が正しいことにはならない。
例えば、コインを投げて1回目に表、2回目に表、3回目に表、4回目に表、5回目に表
と連続して出た場合、それぞれの確率は、1回目は、0.5、2回目は0.25、3回目は0.125、4回目は0.0625,
5回目は0.0312となり、普通、確率が5%を切ったら偶然ではない可能性が大きい。
相関と回帰
相関関係とは、XとYの相関では、Xが大きければ、Yが大きい。
または、Xが小さいほど、Yが小さいなどの関係が明白である。
相関(Correlation)は、2変数(x,y)を区別せずに対等に扱う。
一方が増えたときに他方が増える(減る)の関係性を調べる。
因果関係とは、Xの変化・差でYの変化・差が生じる。
回帰(regression)は、変数(x)で変数(y)を説明する
一方から他方が決定される様子や程度を調べる。
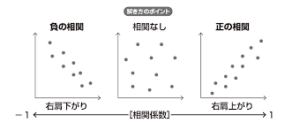
2変量の関係を散布図から視覚化する。
ー>相関関係(正負の一方の直線が)が存在するかを確認する。
ー>相関係数を確認する
相関係数>0で正の相関、相関係数<0で負の相関
総関係数 =0 相関なし
相関係数は、-1から1の値を取る。
相関関係の値を評価:
0.7 以上 津容易相関あり
0.5以上かつ0.7以下 は相関あり
0.3以上かつ0.5以下は、弱い相関あり
0.3以下は相関なし
相関関係(correlation)があるからといって、必ずしも因果関係(causality)があるわけでない

単回帰分析は一つの変数で別の変数を説明する
一方、重回帰分析は、説明変数を複数用いて回帰を行う。
単回帰では直線であったが、重回帰では、平面を描く。
説明変数が質的変数の場合は、ダミー変数を加える。
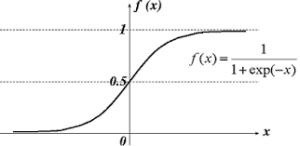
ロジスティック回帰|質的変数を説明するモデル。
ー>シグモイド関数(0から1の間をとる)を使って変換する。
因果推論
因果関係は、以下の3つの条件をすべて満たす。
(1)時間的先行性
ー>原因となる現象が結果となる現象に時間的に先立って起きている。
(2)共変関係
ー> 原因となる現象が変動すると、結果となる現象も変動する。
(3)他条件の同一性
ー> 原因となる現象と結果となる現象の双方に与える現象は、存在しないか、
その影響は統制されている。
実社会ではランダム比較試験は困難である。
操作変数法
回帰不連続デザイン
マッチング
差の差の分析法
重回帰分析


